nLab color branes and flavor branes
Context
String theory
Ingredients
Critical string models
Extended objects
Topological strings
Backgrounds
Phenomenology
Fields and quanta
fields and particles in particle physics
and in the standard model of particle physics:
matter field fermions (spinors, Dirac fields)
| flavors of fundamental fermions in the standard model of particle physics: | |||
|---|---|---|---|
| generation of fermions | 1st generation | 2nd generation | 3d generation |
| quarks () | |||
| up-type | up quark () | charm quark () | top quark () |
| down-type | down quark () | strange quark () | bottom quark () |
| leptons | |||
| charged | electron | muon | tauon |
| neutral | electron neutrino | muon neutrino | tau neutrino |
| bound states: | |||
| mesons | light mesons: pion () ρ-meson () ω-meson () f1-meson a1-meson | strange-mesons: ϕ-meson (), kaon, K*-meson (, ) eta-meson () charmed heavy mesons: D-meson (, , ) J/ψ-meson () | bottom heavy mesons: B-meson () ϒ-meson () |
| baryons | nucleons: proton neutron |
(also: antiparticles)
hadrons (bound states of the above quarks)
minimally extended supersymmetric standard model
bosinos:
dark matter candidates
Exotica
Contents
Idea
In geometric engineering of quantum field theory in intersecting D-brane models the gauge theory which is thought to appear on coincident D-branes (see at gauge enhancement) may play two different roles:
-
color – it may be a Yang-Mills theory of an “actual” gauge field (carried by gluons) coupled to color charges (carried by quarks) – like quantum chromodynamics;
-
flavor – it may be the (“chiral”) gauge theory of a hidden local gauge field (carried by mesons) coupled to flavor charges (carried by baryons) – like quantum hadrodynamics.
In the first case one speaks of color branes, in the second of flavor branes. Typically one indicates the number of coincident such branes with
-
for the number of color branes, leading (in the absence of orientifolds) to gauge group SU;
-
for the number of flavor branes, leading to flavor-symmetry group (“chiral symmetry”) SU (e.g. isospin for ).
| color charge | flavor charge | |
|---|---|---|
| gauge bosons | gluons (gauge group-local symmetry) | mesons (flavor-hidden local symmetry) |
| fermions | quarks | baryons |
In common constructions of holographic QCD in the large-N limit (large number of color charges) in which the AdS/QCD correspondence applies, color branes are modeled as black branes while flavor branes are modeled as probe branes (Karch-Katz 02).
From Ouyang 03, p. 2:
the important feature seems to be that the added branes must be extended along the radial AdS direction; then, volume factors suppress the dynamics of the NN strings on these “flavor branes”, which then contribute states to the gauge theory with global symmetries rather than gauge symmetries.
Examples
Witten-Sakai-Sugimoto model for quantum chromodynamics
For example, in the Witten-Sakai-Sugimoto model for holographic QCD realized on D4-D8 brane intersections, the D4-branes play the role of color branes while the D8-branes play the role of flavor branes.
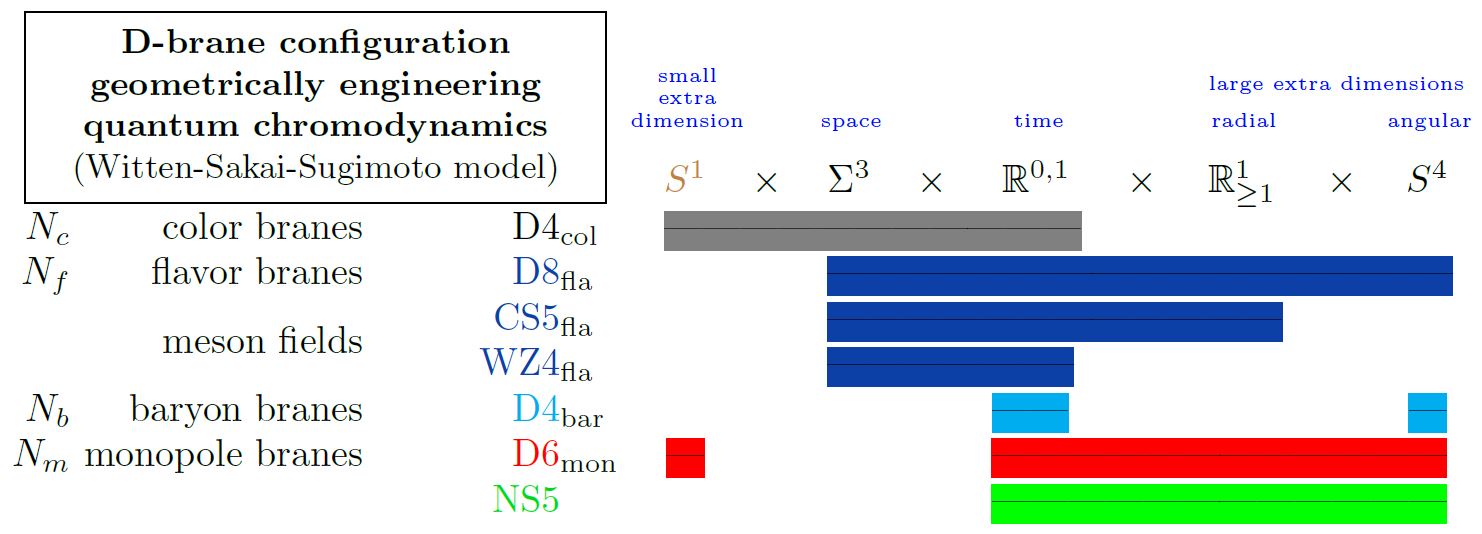
graphics from Sati-Schreiber 19c
Here we are showing
-
with
-
the 5d Chern-Simons theory on their worldvolume
-
the corresponding 4d WZW model on the boundary
exhibiting the vector meson fields in the Skyrmion model;
-
-
(see below at Baryons);
-
the Yang-Mills monopole D6-branes
(see at D6-D8-brane bound state);
-
the NS5-branes (often not considered here).
graphics from Sati-Schreiber 19c
Phenomenology
The geometric engineering of QFT on flavor branes (as in the Witten-Sakai-Sugimoto model) realizes, at least qualitatively, the following experimentall phenomena:
Related concepts
References
General
The concept of flavor branes in the context of holographic QCD properly originates with:
- Andreas Karch, Emanuel Katz, Adding flavor to AdS/CFT, JHEP 0206:043, 2002 (arxiv:hep-th/0205236)
based on the concept of probe branes due to
- Andreas Karch, Lisa Randall, Section 3 of: Open and Closed String Interpretation of SUSY CFT’s on Branes with Boundaries, JHEP 0106:063, 2001 (arXiv:hep-th/0105132)
Other early discussion:
-
Peter Ouyang, Holomorphic D7-Branes and Flavored Gauge Theories, Nucl. Phys. B699:207-225, 2004 (arXiv:hep-th/0311084)
-
Thomas S. Levi, Peter Ouyang, Mesons and Flavor on the Conifold, Phys. Rev. D76:105022, 2007 (arXiv:hep-th/0506021)
-
Carlos Nunez, A. Paredes, A.V. Ramallo, Flavoring the gravity dual of Yang-Mills with probes, JHEP 0312:024, 2003 (arXiv:hep-th/0311201)
See also:
- Daniel Arean, Adding flavor on the Higgs branch, Fortsch. Phys. 56:888-894, 2008 (arXiv:0805.3447)
-flavor symmetry on heterotic M5-branes
Emergence of SU(2) flavor-symmetry on single M5-branes in heterotic M-theory on ADE-orbifolds (in the D=6 N=(1,0) SCFT on small instantons in heterotic string theory):
-
Abhijit Gadde, Babak Haghighat, Joonho Kim, Seok Kim, Guglielmo Lockhart, Cumrun Vafa, Section 4.2 of: 6d String Chains, J. High Energ. Phys. 2018, 143 (2018) (arXiv:1504.04614, doi:10.1007/JHEP02(2018)143)
-
Kantaro Ohmori, Section 2.3.1 of: Six-Dimensional Superconformal Field Theories and Their Torus Compactifications, Springer Theses 2018 (springer:book/9789811330919)
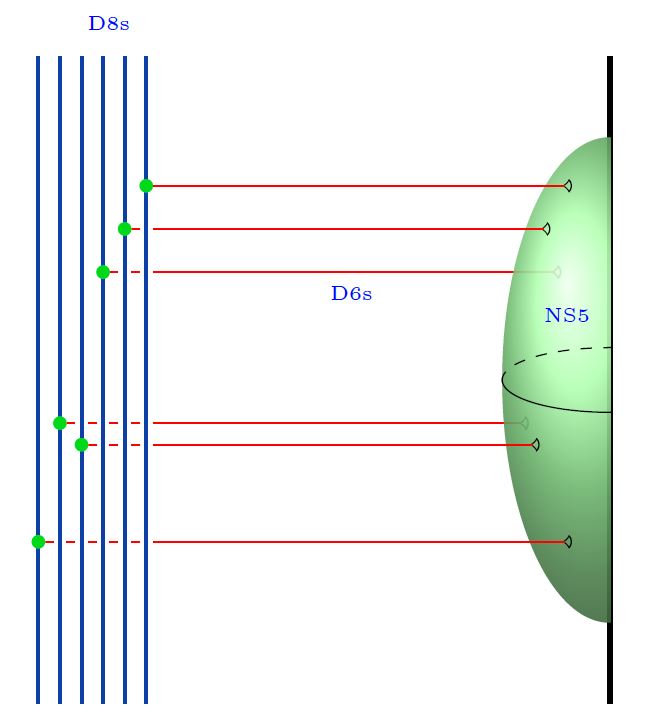
Argument for this by translation under duality between M-theory and type IIA string theory to half NS5-brane/D6/D8-brane bound state systems in type I' string theory:
Reviewed in:
- Santiago Cabrera, Amihay Hanany, Marcus Sperling, Section 2.3 of: Magnetic Quivers, Higgs Branches, and 6d Theories, JHEP06(2019)071, JHEP07(2019)137 (arXiv:1904.12293)
The emergence of flavor in these half NS5-brane/D6/D8-brane bound state systems, due to the semi-infinite extension of the D6-branes making them act as flavor branes:
-
Amihay Hanany, Alberto Zaffaroni, Branes and Six Dimensional Supersymmetric Theories, Nucl.Phys. B529 (1998) 180-206 (arXiv:hep-th/9712145)
-
Ilka Brunner, Andreas Karch, Branes at Orbifolds versus Hanany Witten in Six Dimensions, JHEP 9803:003, 1998 (arXiv:hep-th/9712143)
Reviewed in:
- Fabio Apruzzi, Marco Fazzi, Section 2.1 of: with orientifolds, J. High Energ. Phys. (2018) 2018: 124 (arXiv:1712.03235)
See also:
- Amihay Hanany, Noppadol Mekareeya, The Small Instanton and the Kraft Procesi Transition, JHEP07 (2018) 098 (arXiv:1801.01129)
Last revised on June 14, 2024 at 08:22:22. See the history of this page for a list of all contributions to it.